【水理学：①水圧基礎・発展】せんせいの専門土木速習講座

【無料講義】水理学①水圧基礎・発展

『せんせいの専門土木速習講座』のイメージをつかんでいただくために、第一回の講義は無料で配信させていただきます☺
⇒講義資料(PDF)はこちら

『水圧』の問題も出題頻度は高いです。
問題難易度としては、難しい問題と簡単な問題でムラがありますが、簡単な問題が多いです。また、ココが理解できてないと、他の分野や他の科目にも支障が出てしまうので、基礎はしっかりと固めておいて欲しいなと思います。

【水理学：①水圧基礎・発展】せんせいの専門土木速習講座

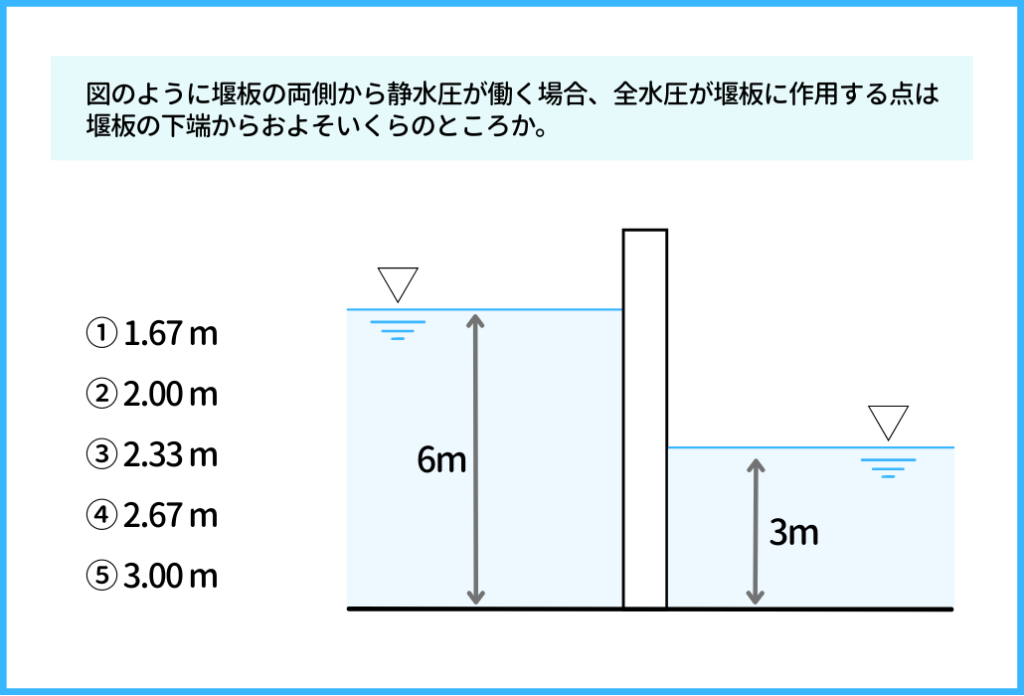
水圧の問題というのは、こういう問題ですね！
様々なタイプの問題がありますので、今回は色々なタイプの問題に触れていけたらと思っております✨

では、この手の問題を解くために必要なポイントから紹介していきたいと思います。

ポイント①：静水圧(水圧)の公式

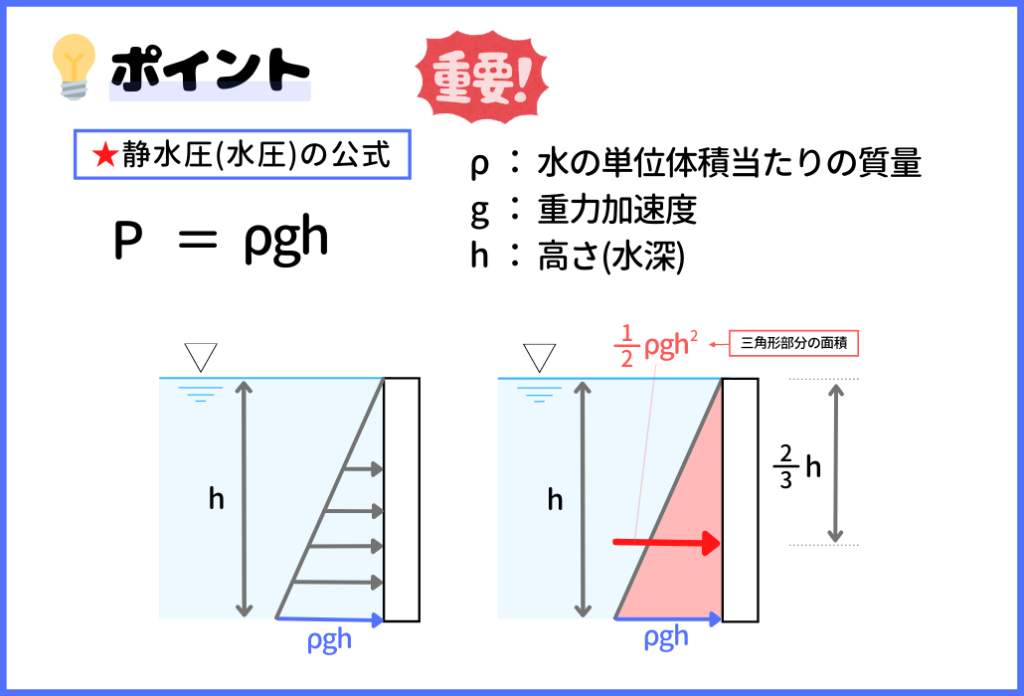
『水圧(静水圧)』というのは、水の重さによる圧力のことです。水の重さですから、深ければ深いほど水圧は大きくなります。

水の密度をρ、重力加速度をgとすると、深さhの時の水圧Pの大きさは、『★P＝ρgh』という式で表されます。

また、水に接する面積全体に作用する水圧の合計を『全水圧』と言います。例えば、図のように、水中の垂直な面に働く全水圧は、三角形分布荷重と同じ考え方で、三角形部分の面積ということになるので、pgh²/2ということになります。そして、三角形なので、水面から2h/3の位置(重心)に力が作用します。

ポイント②：水圧の性質

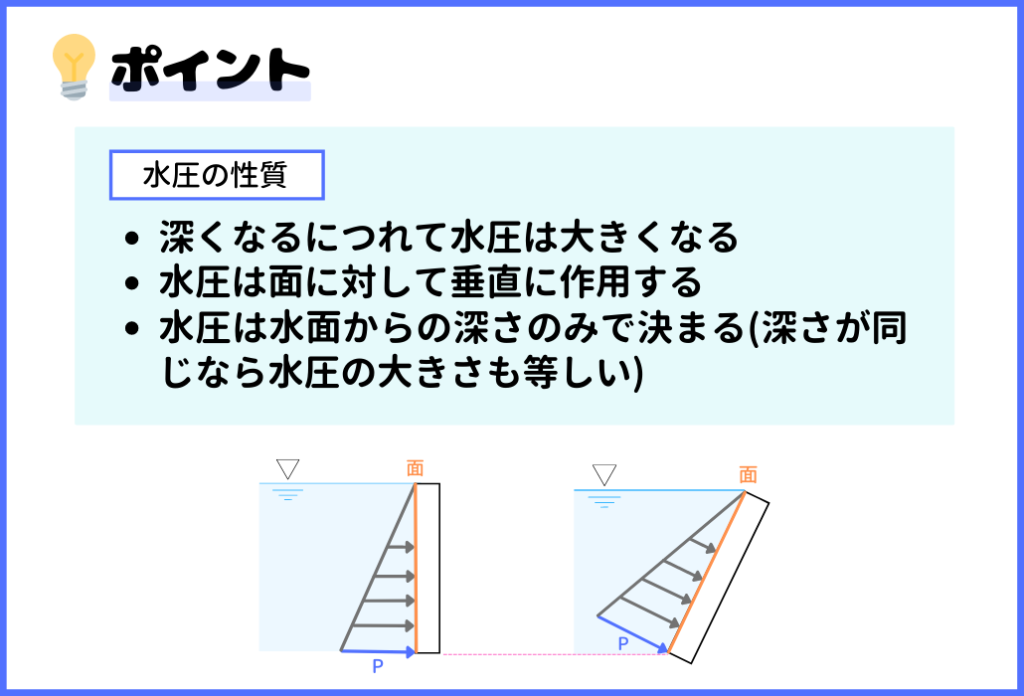
次は、『水圧の性質』について、ポイントを紹介していきます。上記の３つのポイントは絶対に把握しておいてください。

水圧は、面に対して垂直に作用します。例えば、図のように、面が斜めだったとしても、面に垂直になるように水圧が作用します。

また、水圧は水面からの深さのみで決まるという点も重要です。同じ深さであれば、水圧の大きさは等しくなるので、例えば、面が斜めになったとしても、同一水平面上であれば、水圧の大きさ(P)は等しくなります。

ポイント③：傾斜した平面に加わる全水圧

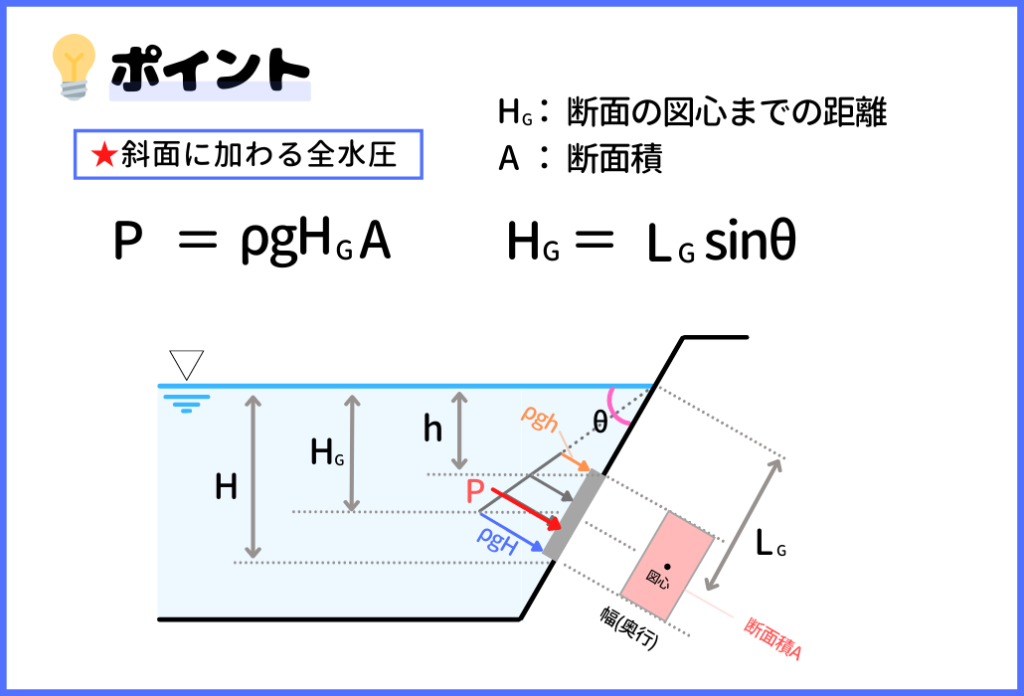
では次は、『傾斜した平面に加わる水圧』の考え方について紹介していきます。

斜面に加わる全水圧Pは、『 P＝ρgH_GA 』という式で表されます。H_Gは断面の図心までの距離で、Ａは断面積です。

そして、斜面部分の図心までの距離をL_Gとすると、H_G＝L_Gsinθという関係が成り立ちます。

また、水圧が台形分布になってしまっていますが、この手のものは三角形部分と四角形部分に分けて考えていきます。

ポイント④：ゲージ圧と絶対圧

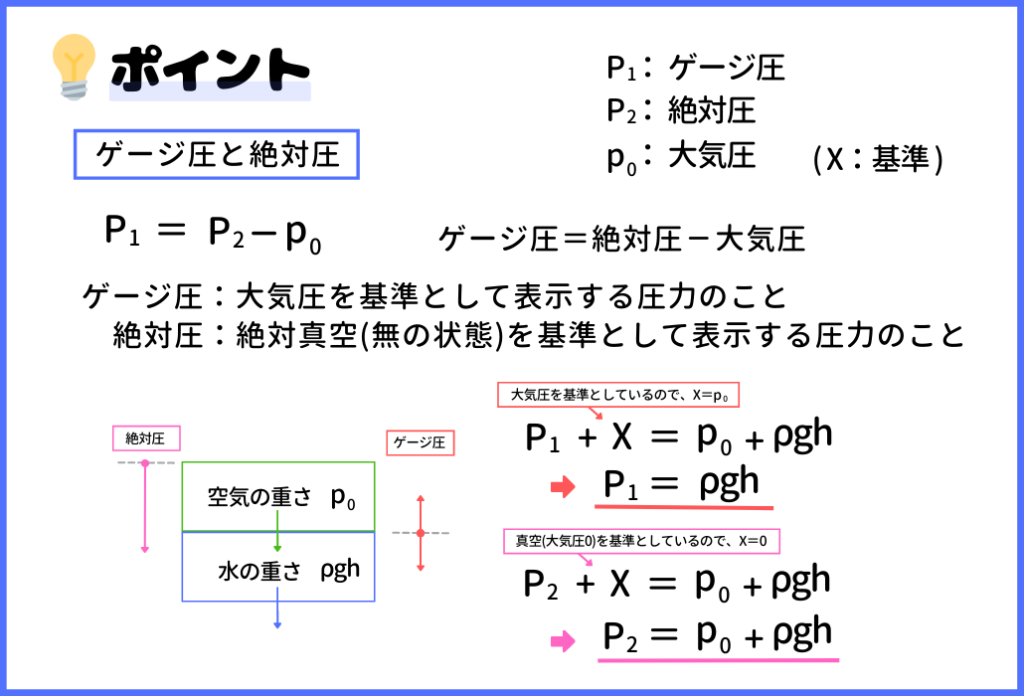
『ゲージ圧』と『絶対圧』の考え方についても紹介させていただきます。

ゲージ圧というのは、大気圧を基準として表示する圧力のことで、絶対圧というのは、真空状態を基準として表示する圧力のことです。
⇒先ほど紹介した公式などは全て、ゲージ圧で示したものです。

皆さん日頃生活していても、空気に重さがあるということはあまり意識しないと思いますが、実は空気にも重さがあって、この重さのことを大気圧と呼びます。
そこで、水中のとある点の水圧について考える際には、本来、空気の重さと水の重さのどちらも考慮する必要があります。
ただ、毎回毎回大気圧を考慮していると面倒くさいので、私たちの普段の生活の中では、基本的に大気圧を基準として、色々な圧力を表示しています。なので、基本的には水理学の問題も『ゲージ圧』を使用します。問題文に『真空』を基準とするなどの表記がある場合は、絶対圧の考え方で問題を解いていってください。

ポイント⑤：テンター(ラジアル)ゲート（曲面に水圧が作用）

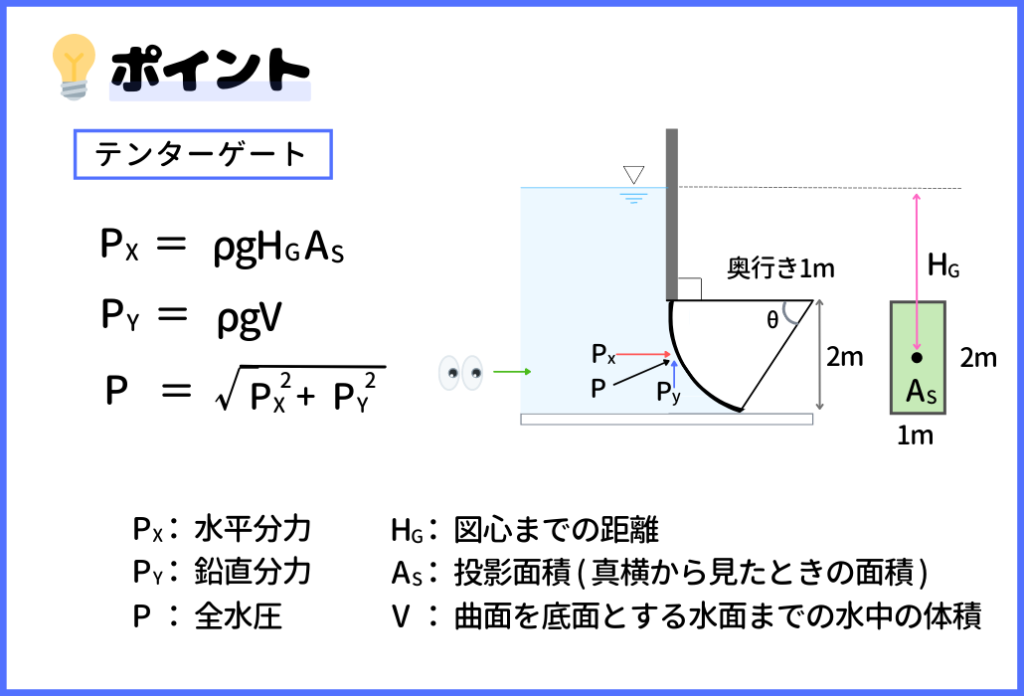
では、次は『テンターゲート』についてポイントを紹介していきます。

この手の曲面に働く問題が出たら、全水圧Pを、水平方向と鉛直方向に分けて考えていきます。
そこで、水平分力は、『 P_X＝ρgH_GA_S 』という式で表され、鉛直分力は、『 P_Y＝ρgV 』という式で表されます。そして、三平方の定理より、『 P＝√P_X²＋P_Y² 』という関係になります。

また、A_Sというのは、投影面積のことで、単純に緑の矢印の方向から見たときの断面の面積のことです。そして、H_Gが水面から投影図の図心までの距離のことです。

公務員試験に出てくる水圧の問題は、今回紹介した５つのポイントを理解していればだいたい解けます！
ということで、今回は例題を７問紹介します！

【水理学：①水圧基礎・発展】過去問を解いてみよう！

【例題①】過去問を解いてみよう！

先ほど紹介したこちらの問題を解いていきます。ちなみに、この問題は地方の試験で実際に出題された問題です。

【例題①】過去問の解説

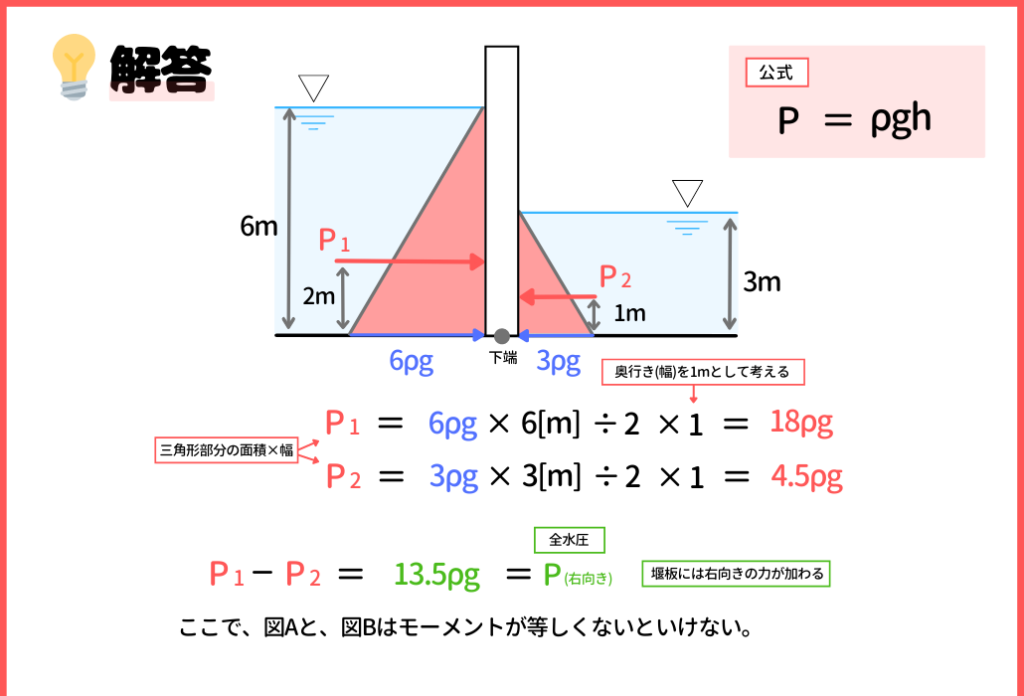
まず、公式より、青色矢印の大きさは、それぞれ、6ρg、3ρgであることがわかります。
そして、三角形分布荷重の合力は、三角形部分の面積となるので、P₁の方が、6ρg×6÷2×1で18ρg、P₁の方が、3ρg×3÷2×1で4.5ρgになります。

ココで荷重の合力を計算すると、P₁ーP₂で、13.5ρgということで、右向きに力が加わっている状態となります。(※注意点なのですが、力が釣り合っているわけではないので、ココは気を付けて下さい。)

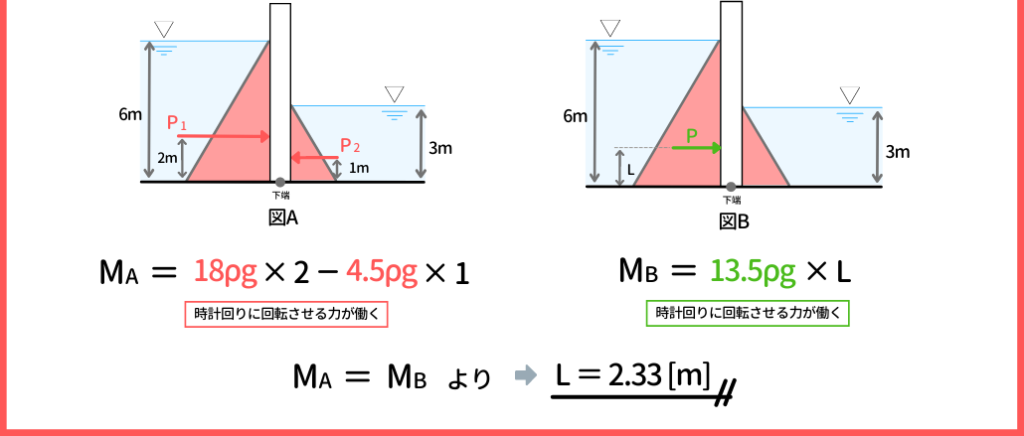
求めたい値である、作用位置までの距離をLと置くと、図Bのような状態になります。ここで、図Aと図Bの状態でのモーメントは等しいハズですから、M_A＝M_Bを計算すれば、L=2.33mということが分かります。

答えは『 ③ 2.33m 』ですね！

ちょっと難しく感じた方もいるかもしれませんが、この手の問題は全て同じ解法で解けますので、解けなかった方は、解法手順を覚えておいてください。

【例題②】過去問を解いてみよう！

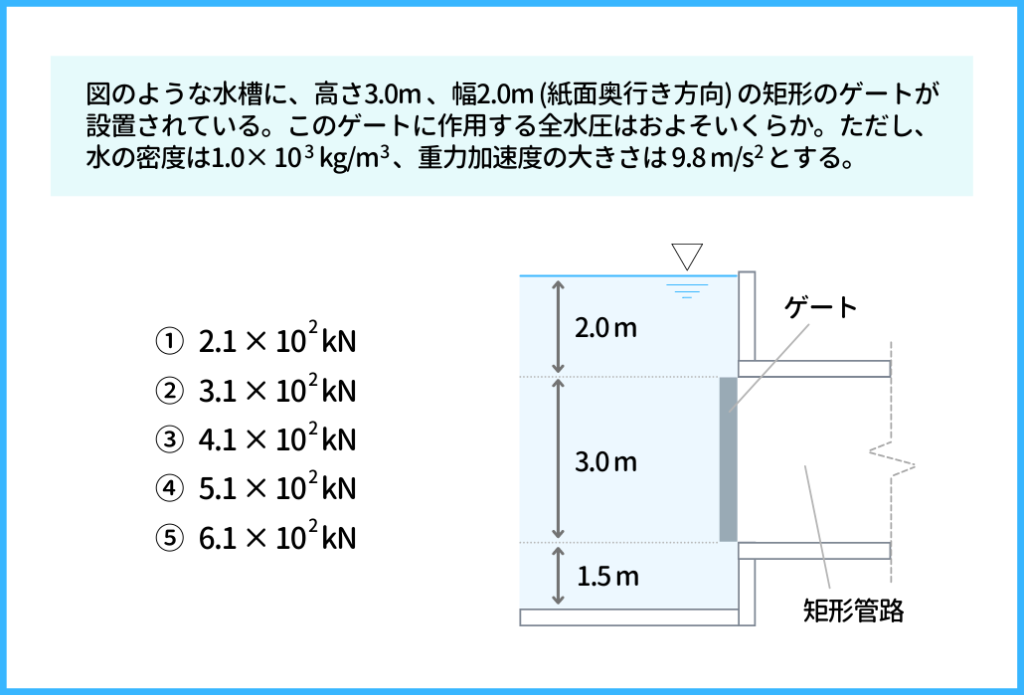
では次の問題を解いていきます。こちらは国家一般職の試験で実際に出題された問題です。

【例題②】過去問の解説

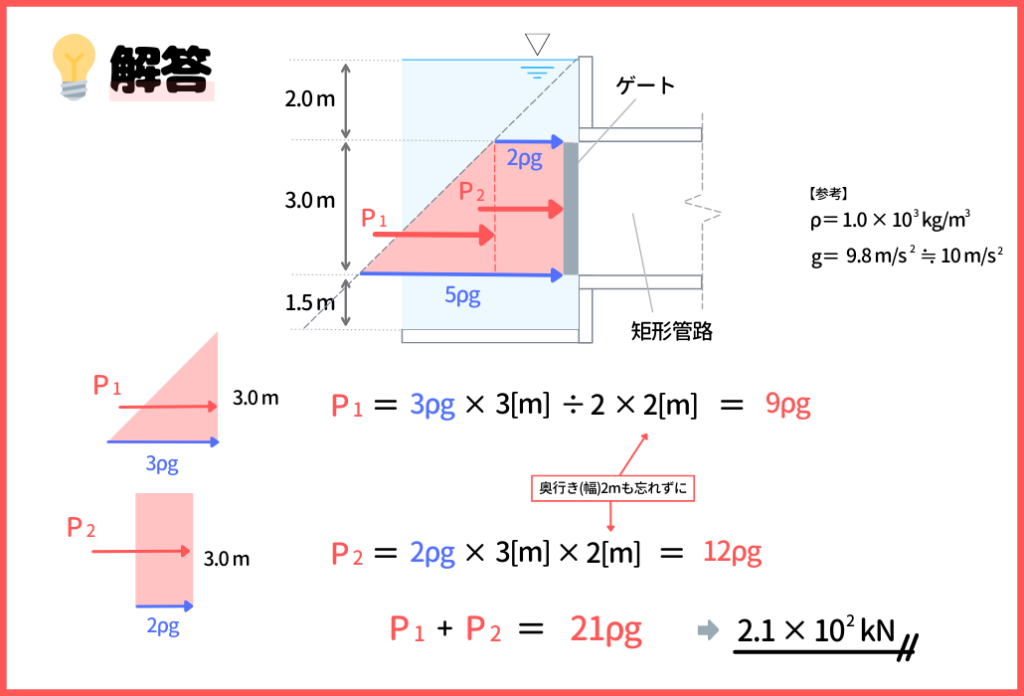
まず、水圧分布を図示すると、こちらのように台形分布になります。台形の場合は、三角形部分と、四角形部分に分けて考えればOKです！

台形の上底が2ρgで、下底が5ρgになるので、三角形部分の青矢印は3ρgで、四角形部分の青矢印は2ρgになります。

この面積が力の大きさですから、それぞれ計算すると、P₁が9ρg、P₂が12ρgとなります。全水圧は、P₁をP₂を足したものになるので、答えは2.1×10²kNということで、答えは『 ① 2.1×10²kN 』です。

また、選択肢を見てもらったらわかると思いますが、厳密に計算しないと正解が絞れないような問題ではありません。重力加速度は9.8m/s²という値になっていますが、大体10m/s²ということで、計算してもらえればと思います。コレは取りたい一問です！

【例題③】過去問を解いてみよう！

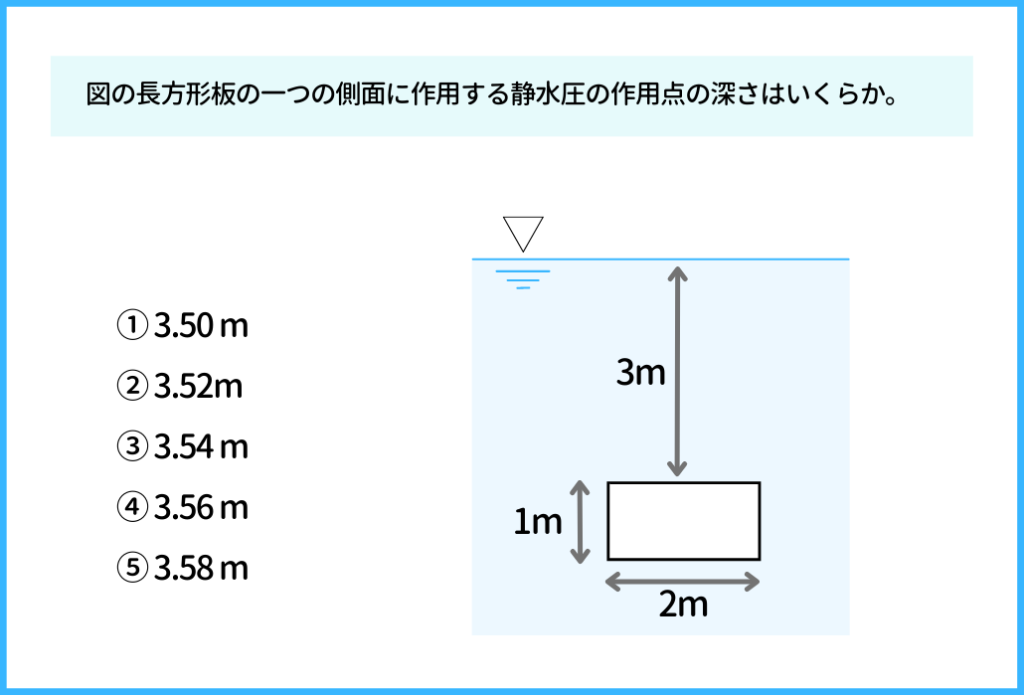
こちらは地方の試験で出題された有名な問題です。

【例題③】過去問の解説

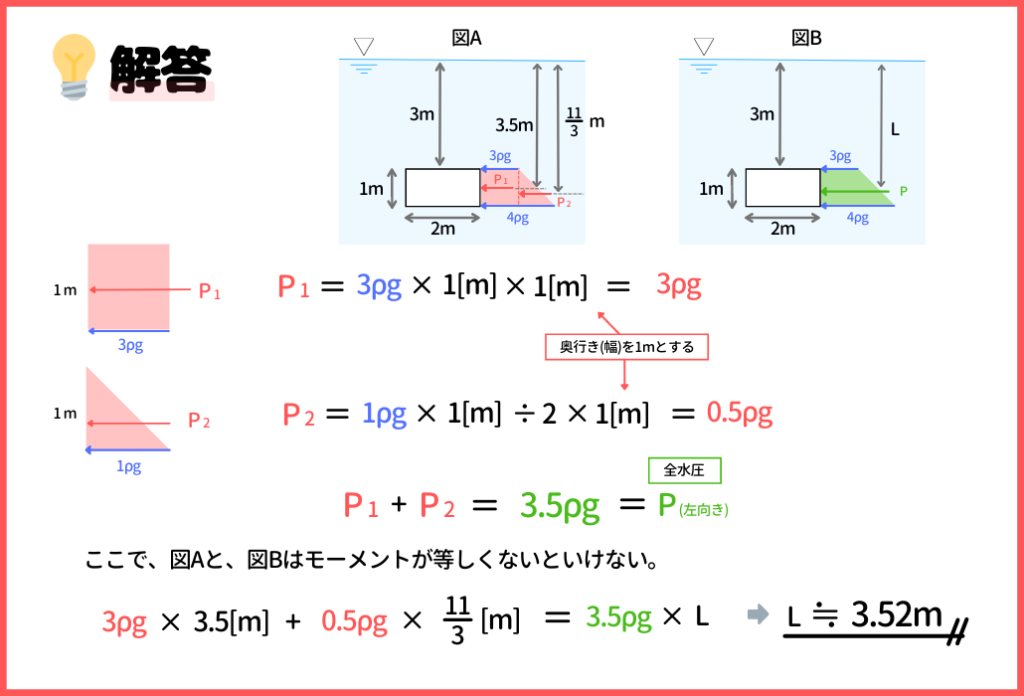
まず、板に作用する水圧は台形分布になります。そして、台形分布の時は三角形部分と四角形部分に分けて考えていきます。

ここで、上底が3ρg、下底が4ρgなので、四角形部分の面積は3ρg、三角形部分の面積は0.5ρgで、奥行きを1mとするとそれぞれ大きさは3ρg、0.5ρgと表せます。

そして、全水圧Ｐは、P₁＋P₂なので、3.5ρgとなります。

水面からP₁までの距離は3.5m、水面からP₂までの距離は11/3mです。また、水面から全水圧Pまでの距離をLとします。

図Ａ、図Ｂのモーメントは等しくなるはずですから、図Ａのモーメント＝図Ｂのモーメントを解くと値は3.52mとなるので、答えは『 ② 3.52m 』ですね！

【例題④】過去問を解いてみよう！

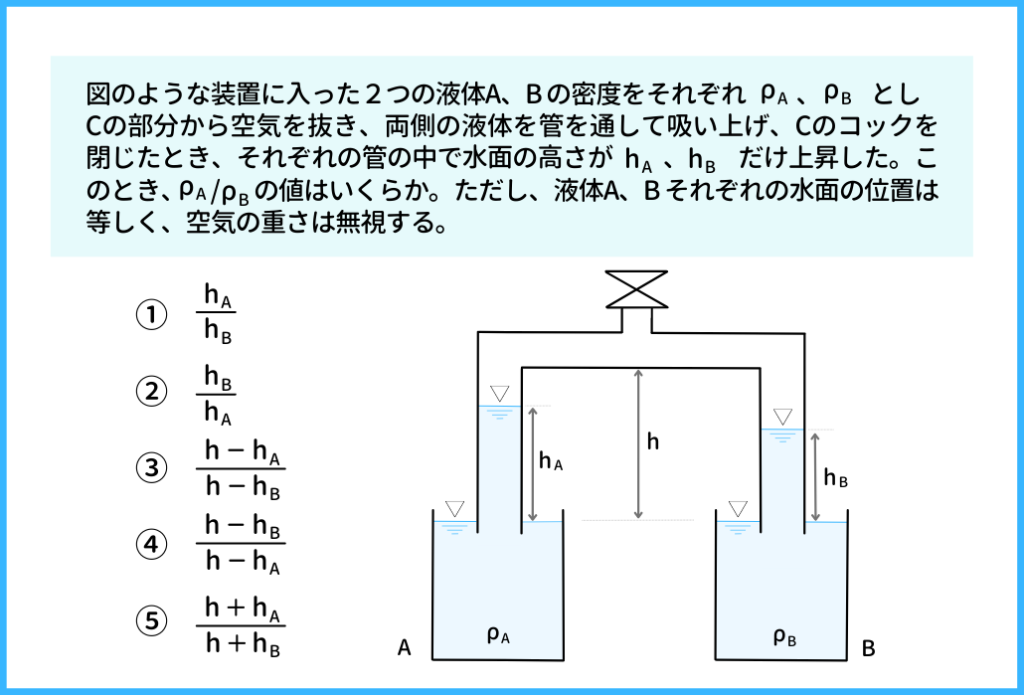
こちらも地方の試験で出題された問題です。

【例題④】過去問の解説

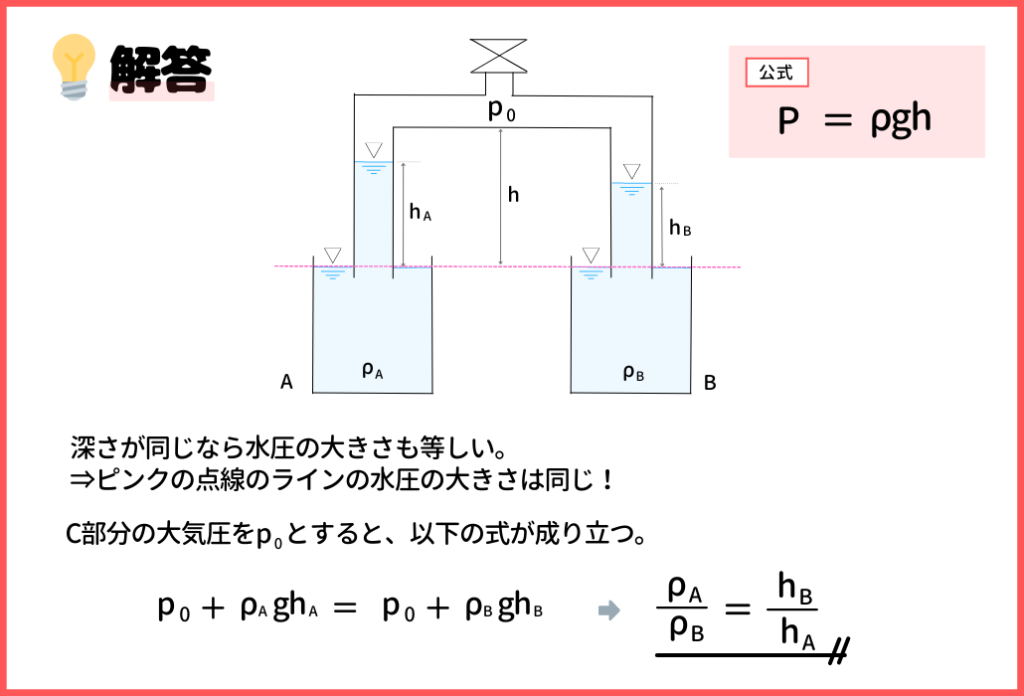
『深さが同じなら水圧の大きさも等しい』という、水圧の性質が理解できているかいないかを問う問題ですね。

ピンクの点線ラインの水圧の大きさは等しくなるハズ。そして、Ｃ部分の圧力をp₀とすると、P₀＋ρ_Agh_A＝p₀＋ρ_Bgh_Bという式が成り立ちますので、ρ_A/ρ_Bの値はh_B/h_Aだとすぐに気づけます。

ということで、答えは『 ② h_B/h_A 』ですね！

【例題⑤】過去問を解いてみよう！

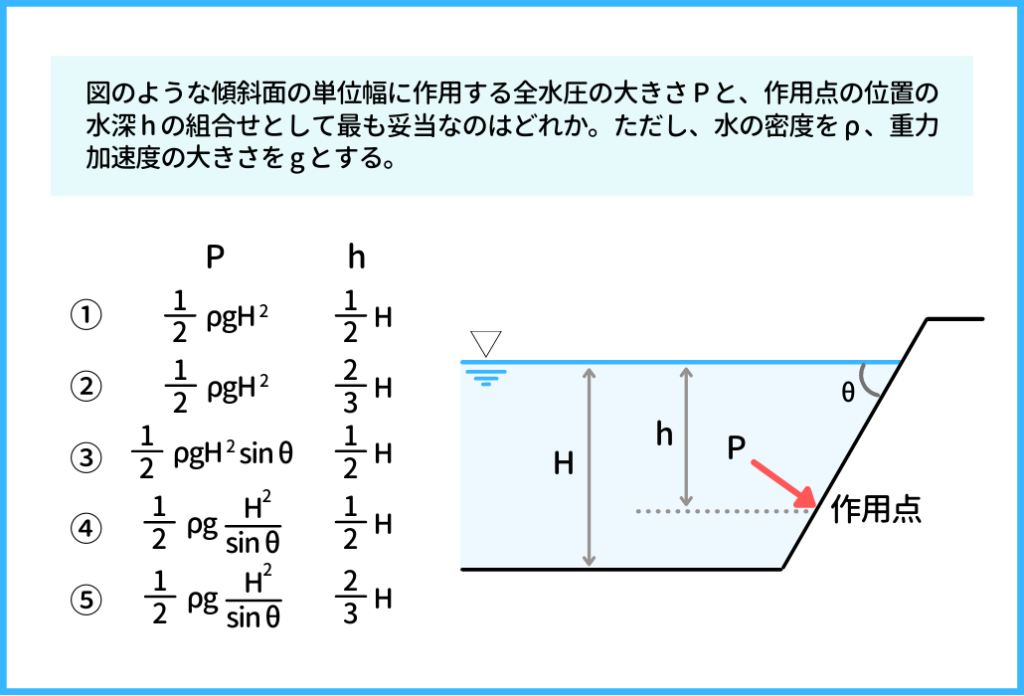
こちらは国家一般職の試験で出題された問題です。

【例題⑤】過去問の解説

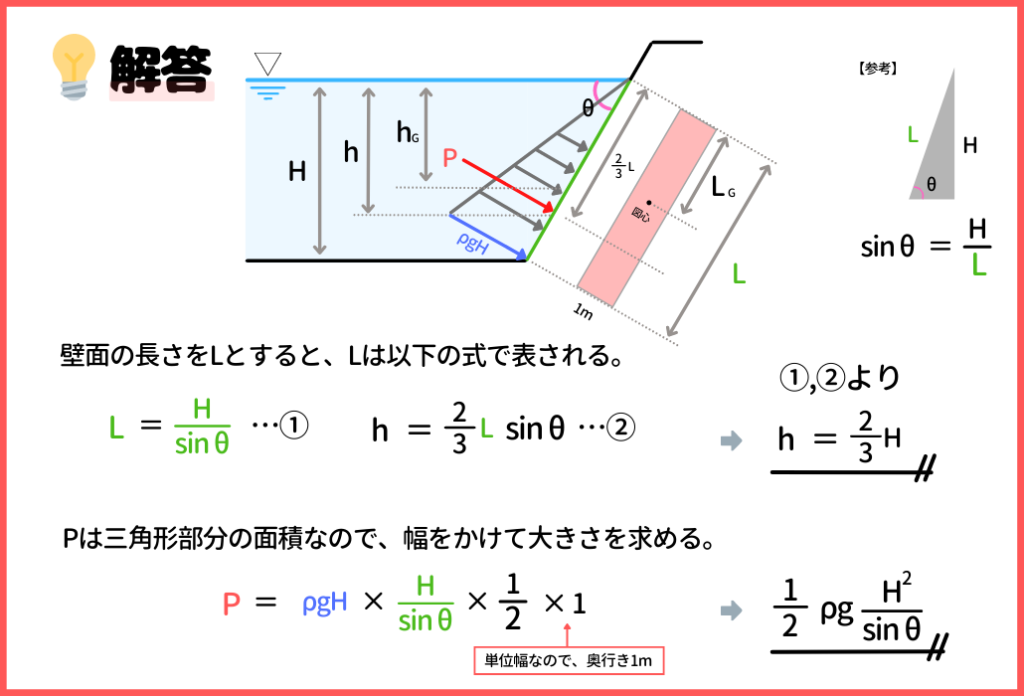
まず、三角形分布の場合は、力は重心に作用するので、作用位置は斜面でも2H/3であることはすぐに判断できると思います。この段階で正解の肢は②か⑤になります。

一応、きちんとhを求めると、sinθ＝H/Lより、L＝H/sinθであることがわかります。そして、h＝2L/3×sinθなので、①②式より、h＝2H/3とhの大きさが求まります。

次にPの大きさを求めていきます。
『深さが同じなら水圧の大きさも等しい』という性質から、青矢印の大きさがρgHであることに注意して計算するだけです。
三角形部分の面積が全水圧の大きさなので、ρgH×H/sinθ×1/2×1ということで、答えは『 ⑤ Ｐ＝1/2×ρgH²/sinθ：h＝2H/3 』ですね！

【例題⑥】過去問を解いてみよう！

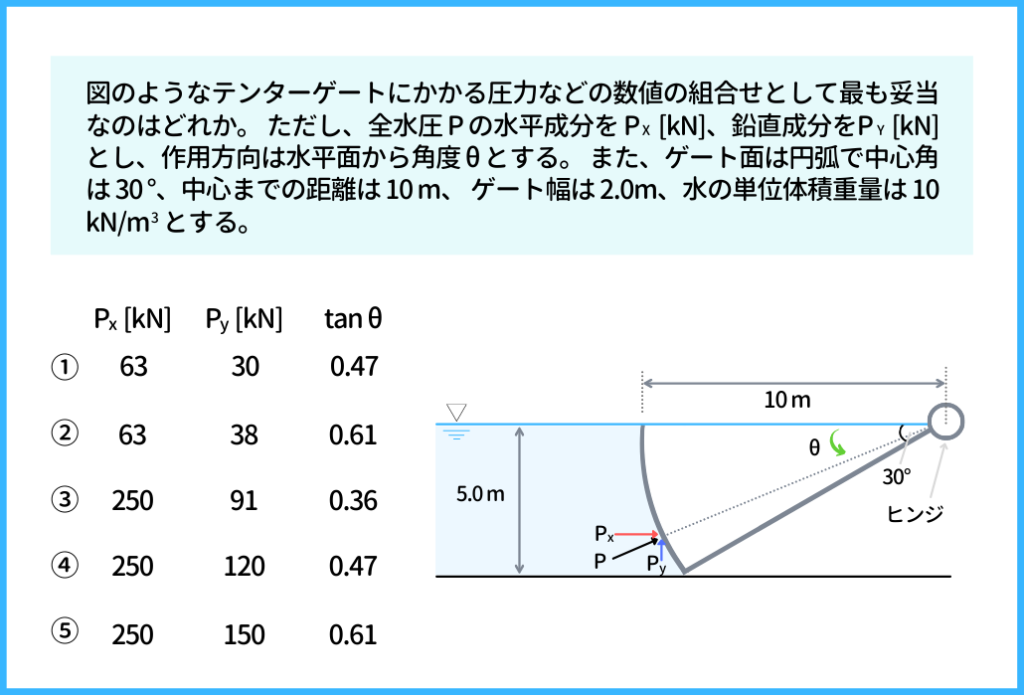
こちらも国家一般職の試験で出題された問題です。

【例題⑥】過去問の解説

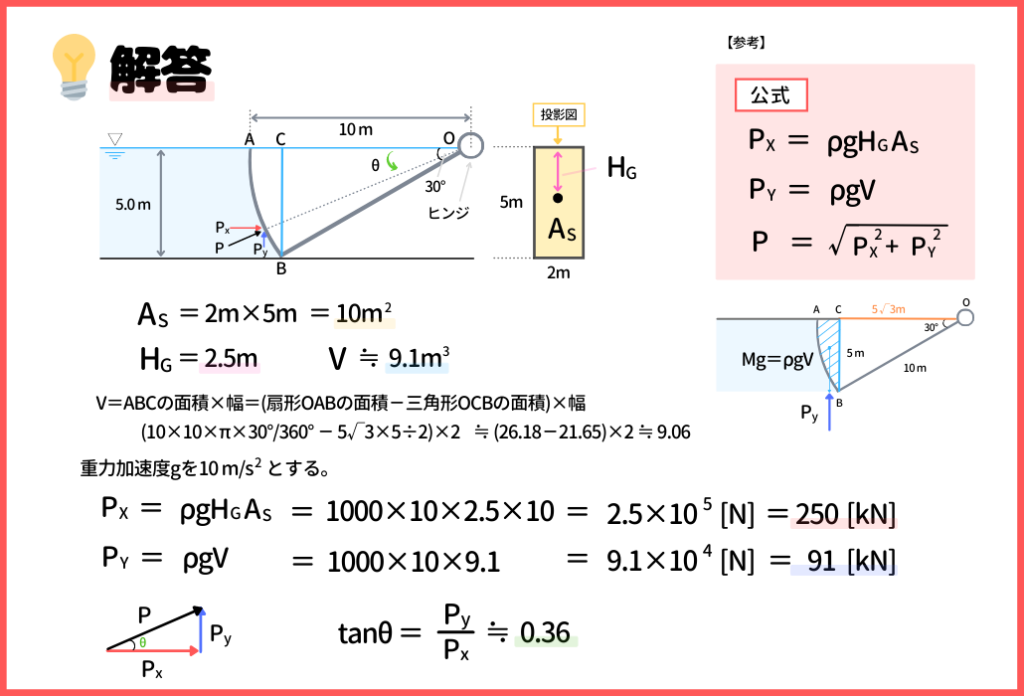
テンターゲートの問題が出たら、まずは公式を思い出します。
この問題の場合は、投影面積A_Sは、10m²で、図心までの距離H_Gは2.5mであることはすぐに判断できると思います。

体積Vの考え方が複雑なのですが、Ｖというのは、図のABCの体積のことです。
なので、扇形OABの体積から、三角形OCBの体積を引き算すれば求めたい値が求まります。
計算すると、ABCの体積は、大体9.1m³になります。

ココまで整理出来れば、後は公式に当てはめて計算するだけです。

P_Xが、ρgH_GA_Sなので、計算すると、250kN
P_Yが、ρgVなので、計算すると、91kNになります。
そして、tanθはP_Y/P_Xなので、0.36くらいになります。

ということで、答えは『 ③ 250kN：91kN：0.36 』ですね！

【例題⑦】過去問を解いてみよう！

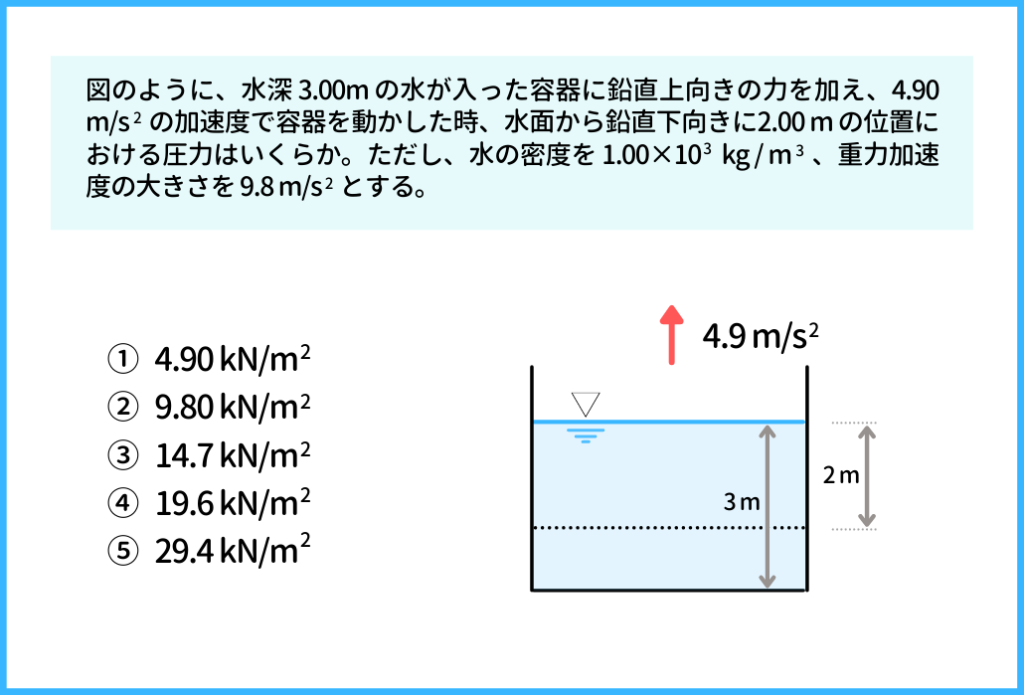
こちらも国家一般職の試験で出題された問題です。物理的な知識も必要とする問題です。

【例題⑦】過去問の解説

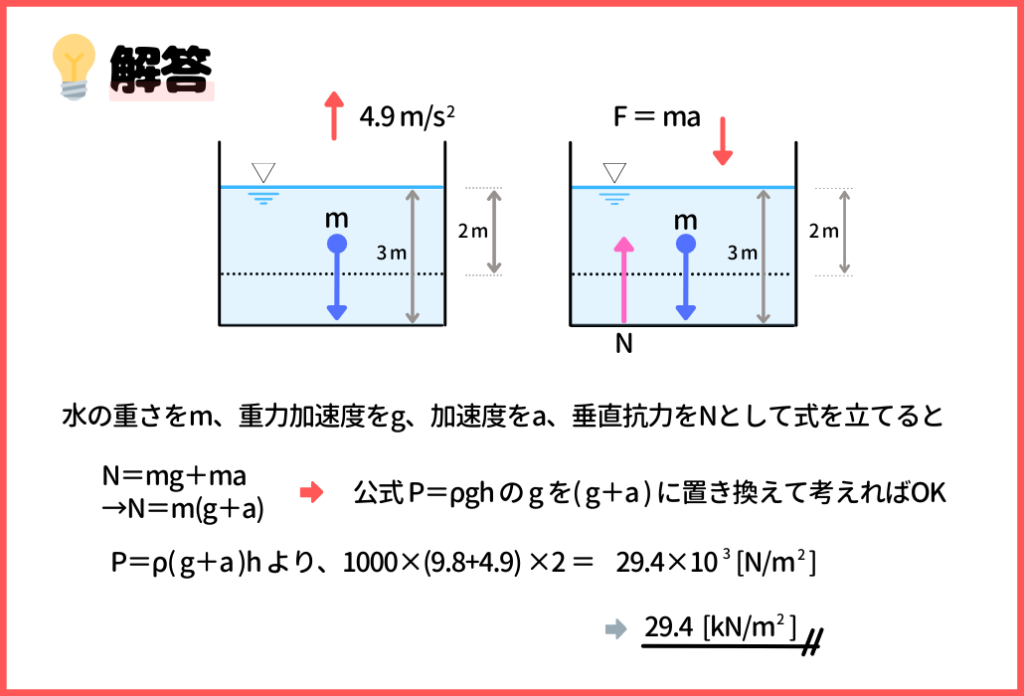
慣性力の公式は「F=－ma」で、大きさ自体は「ma」です。
ｍ：質量、a：加速度

なぜマイナスがつくのかというと、慣性力という力は加速度と反対方向に作用するからです！
(ちなみに、mというのは、ρ×Vのことで、Vは面積×奥行きになります。)

そこで、水の重さをm、重力加速度をg、加速度をa、垂直抗力をNとして式を立てると、N＝m(g＋a)という式が成り立ちます。
⇒なので、水圧の公式のρghの普段使っているgの部分を(g+a)に置き換えて、計算すれば答えが求まります。

計算すると、29.4kN/m²となるので、答えは『 ⑤ 29.4kN/m² 』ですね！

加速度が無かった時の2mの位置での圧力は19.6kN/m²になります。上向きに容器を動かしているわけですから、水が下向きに加える力が大きくなることは容易に想像できるので、この考え方を知っているだけでも答えが⑤であることは判断できます。
なので、実は上昇するエレベーターに乗っている最中に体重を計ると、本来の体重より重くなります。

コメント

はい、ではコレで水圧の講義は終わりです。
難しく感じた方もいると思いますが、今回伝えた5つのポイントをきちんと理解することができれば、公務員試験に出てくる水圧の問題は大体解けると思います。
なので、わからなかった部分はきちんと復習しておくようにしましょう！
では、本日もありがとうございました。

前のテーマを勉強 | トップメニューに戻る | 次のテーマを勉強