【無料講義】構造力学①不静定次数

- 構造力学:①不静定次数
- 重要度:★★★★★
- 難易度:★☆☆☆☆
【構造力学:①不静定次数】せんせいの専門土木速習講座
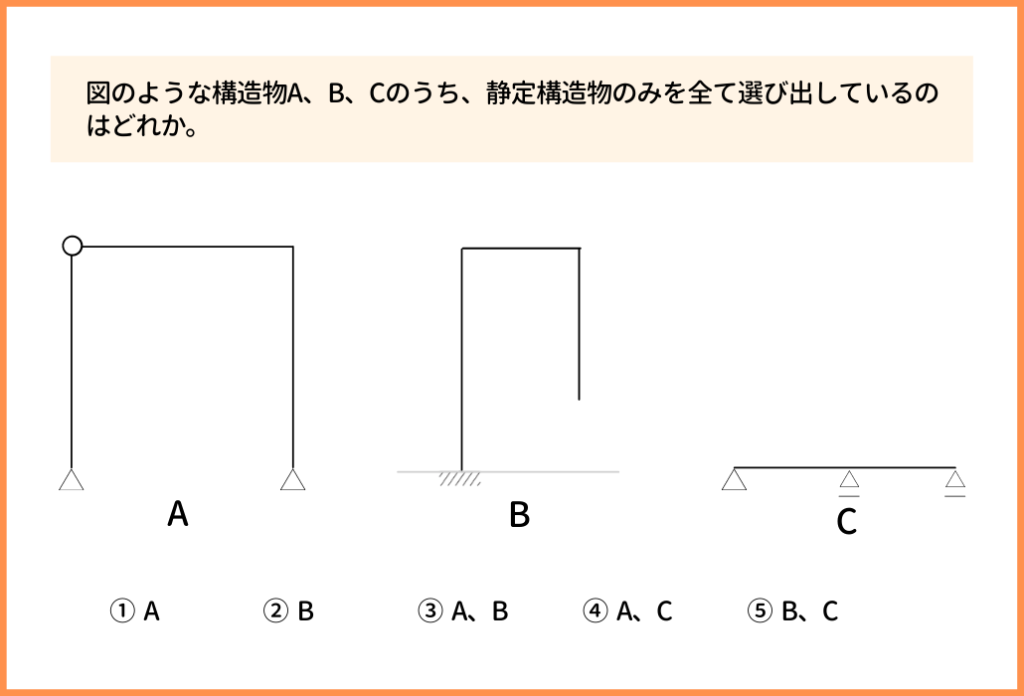
まず初めに言っておきます。
この手の問題が出たら絶対に正答させなければいけません!
めちゃくちゃ簡単ですし、割と試験に出るので、『出たらラッキー』と思えるテーマです。

ポイント①:支点とは?
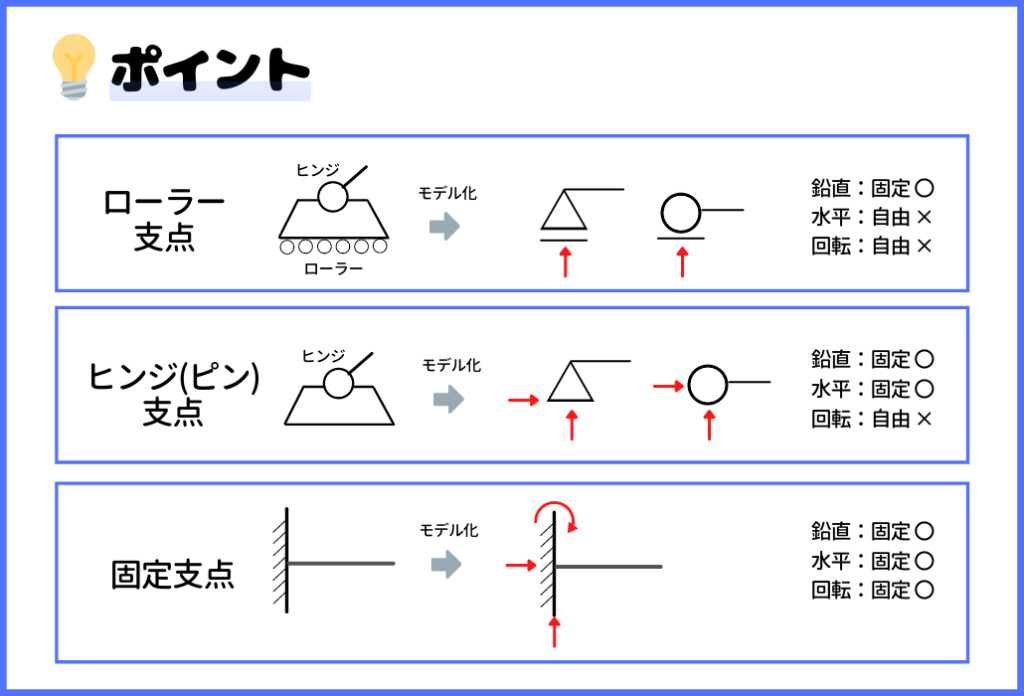
支点というのは、単純に建物を支える点のことで、主に上記の3つが代表的なものとして挙げられます。

『支点』の考え方については、これから構造力学の問題を解くために絶対に覚えておかなければいけない考え方といっていいでしょう。めちゃくちゃ重要です!
まぁご存じいただけている方も多いと思いますので速習講座では詳しく紹介しませんが、不安な方はブログの方で復習の意味も込めて、もう一度それぞれの支点の考え方についてチェックしておいてください!
ローラー支点とは
ローラー支点というのは、その名の通りで、ローラースケートをイメージしてもらえればいいと思います。
- 鉛直は固定:人間の重力に耐えることができているので、鉛直方向の力には耐えられます。
- 水平は自由:コロコロ転がるわけですから、水平方向の力には耐えられません。
- 回転は自由:人間の足首がヒンジだとすると、足首を支点として人間の体は自由に傾けられますので、自由に回転させることができます。
ヒンジ(ピン)支点とは
こちらはドアの蝶番(ちょうつがい)をイメージしてもらえればと思います。
(宝箱の上と下の境目の部分)
- 鉛直は固定:縦にガチャガチャ力を加えても動きません。鉛直方向の力には耐えられます。
- 水平は固定:横にガチャガチャ力を加えても動きません。水平方向の力には耐えられます。
- 回転は自由:ドアは蝶番を起点として自由に傾けられますので、自由に回転させることができます。
固定支点とは
こちらは単純に棒を壁にぶっさしたものをイメージしてもらえればと思います。
- 鉛直は固定:縦にガチャガチャ力を加えても動きません。鉛直方向の力には耐えられます。
- 水平は固定:横にガチャガチャ力を加えても動きません。水平方向の力には耐えられます。
- 回転は固定:傾けようと思っても抵抗があります。回転させる力にも耐えられます。

なのでココはきちんと理解しておいてください。
ポイント②:構造物の分類
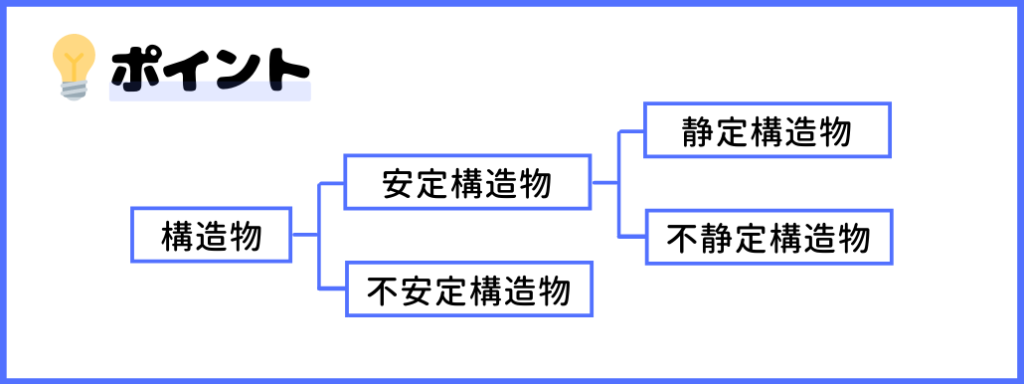
2つ目のポイントは、構造物の分類です。
構造物は、安定構造物と不安定構造物に、そして安定構造物は静定構造物と不静定構造物に分けられます。

安定構造物とは?
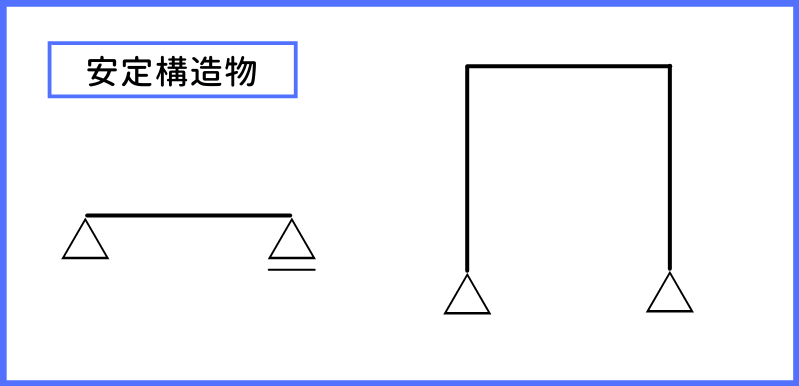
外力が作用してもただちに崩壊しない構造物のことを『安定構造物』といいます。(力学的に安定しています)
わけわからないかもしれませんが、日頃皆さんが目にする、橋やビルなどの建築物は基本的にすべて『安定構造物』です。

不安定構造物とは?
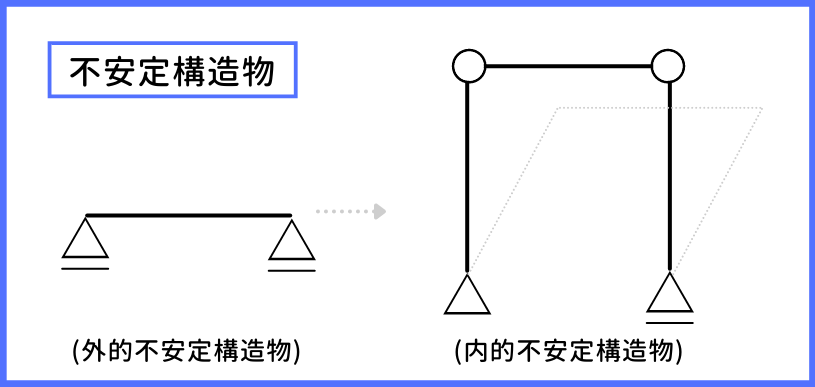
外力が作用した時にただちに移動、変形してしまう構造物を『不安定構造物』と言います。
簡単に言うと、自立できない構造物のことですね!
⇒力のつり合いが取れてない!


右はちょっと押しただけでバタンと倒れちゃいそう!
静定構造物とは?
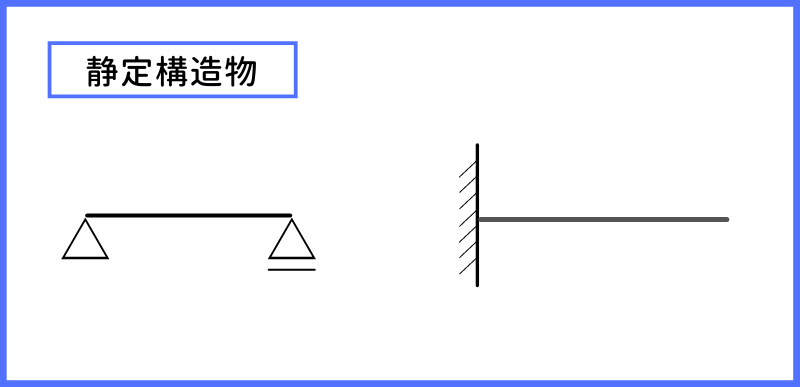
『静定構造物』というものは、安定構造物の中で、3つの力のつり合いの条件式(∑V=0、∑H=0、∑M=0)で反力や断面力が求められるものを指します。

不静定構造物とは?
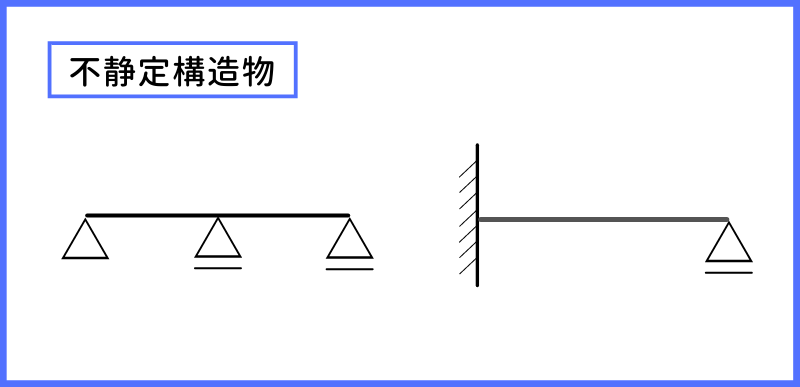
反対に『不静定構造物』というものは、安定構造物の中で、3つの力のつり合いの条件式(∑V=0、∑H=0、∑M=0)で反力や断面力が求められないものを指します。
(変形の適合条件を考慮する必要がある)

見方を変えると、『余裕を持って安定している状態』にある構造物のことです!
⇒なので、その辺のビル等も不静定構造物であることがほとんどです。
ポイント③:構造物の分類の公式

今日この講義で覚えて欲しい一番重要な公式が『不静定次数の公式』です!
拘束度の注意点
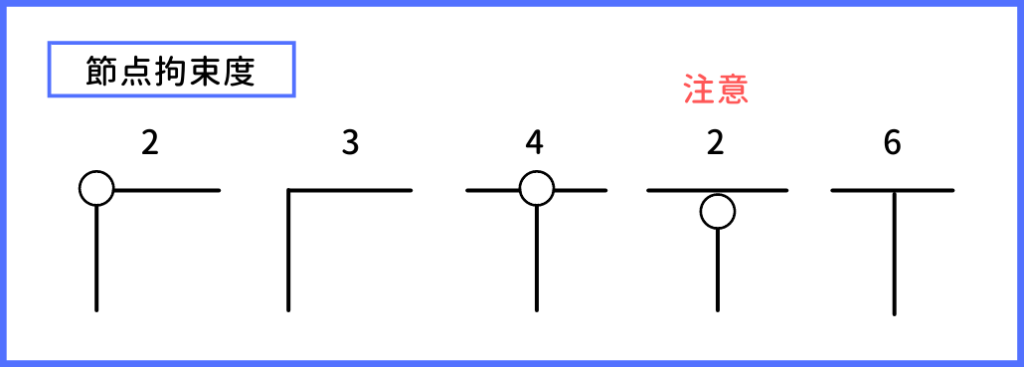
支点(節点)における拘束度の度合いを『拘束度』と言います。(拘束度=反力数)
(単純に反力数と等しいので、例えば、ヒンジはモーメント以外が拘束されるので、拘束度2です。)
また、上部材は節点として考えないので、この点だけ気を付けて下さい。

まぁ公務員試験の場合は、難しいことは考えなくてOKです!
公式の使い方を覚えて問題が解ければOKなので、さっそく例題を解いていきましょう!
(トラスのポイントもありますが、先に例題1~3を解いていきます。
ポイント④:トラスの静定・不静定の判別公式

トラスの場合は、上記の公式で静定か不静定かを判別します!
地方の試験等でたまに出題されるので、おさえておきたいところではあります。
こちらも実際に問題を解いて慣れていきましょう!
(例題4~5)
【構造力学:①不静定次数】過去問を解いてみよう!
【例題①】過去問を解いてみよう!

先ほど紹介したこちらの問題を解いていきます。
ちなみに、この問題も国家一般職の試験で実際に出題されたものです。

最初なので、色を使って丁寧に解説してきますね!
【例題①】過去問の解説
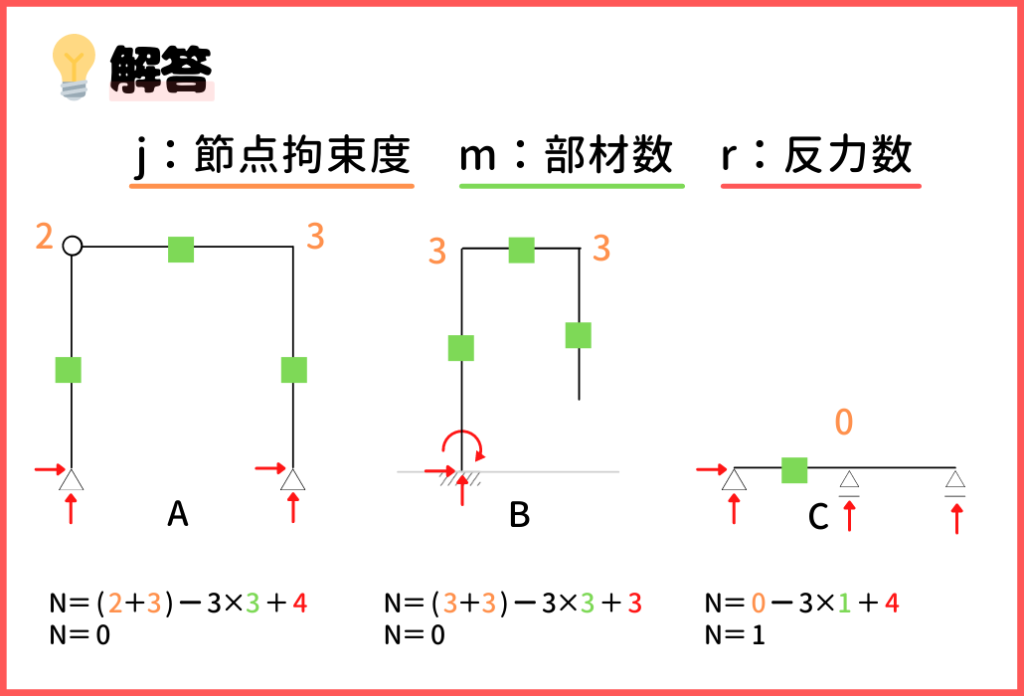
不静定次数の公式は『 N=j -3m + r 』です。
節点拘束度をオレンジ、部材数を緑、反力数を赤で示しています。
節点拘束度は、Aが2+3で5、Bが3+3で6、Cが0
部材数は、Aが3、Bが3、Cが1(Cはまっすぐな棒が一つのみというイメージ)
反力数は、Aが4、Bが3、Cが4(ローラー支点が1、ヒンジ(ピン)視点が2、固定支点が3)

N>0で不静定構造物なので、Cは(1次の)不静定構造物です!
よって、静定構造物のみを選んでいるのは『③ A,B 』ですね!
【例題②】過去問を解いてみよう!
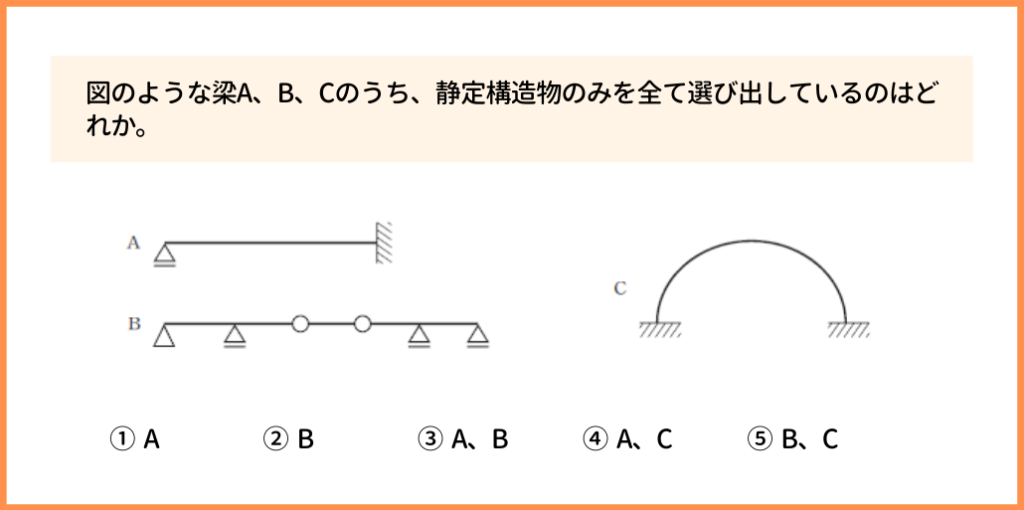
もう1問この手の問題を、今度は自力で解いてみて下さい!
【例題②】過去問の解説
不静定次数の公式は『 N=j -3m + r 』です。
- A:N=0ー3×1+4=1
- B:N=4ー3×3+5=0
- C:N=0ー3×1+6=3
N=0で静定構造物なので、答えは『 ② B 』ですね!

片持ち梁は静定なので、問題を見た瞬間に「Aは静定構造物ではないな」と最低でも気づきたいところです。これに気づくだけで2択になります。
【例題③】過去問を解いてみよう!
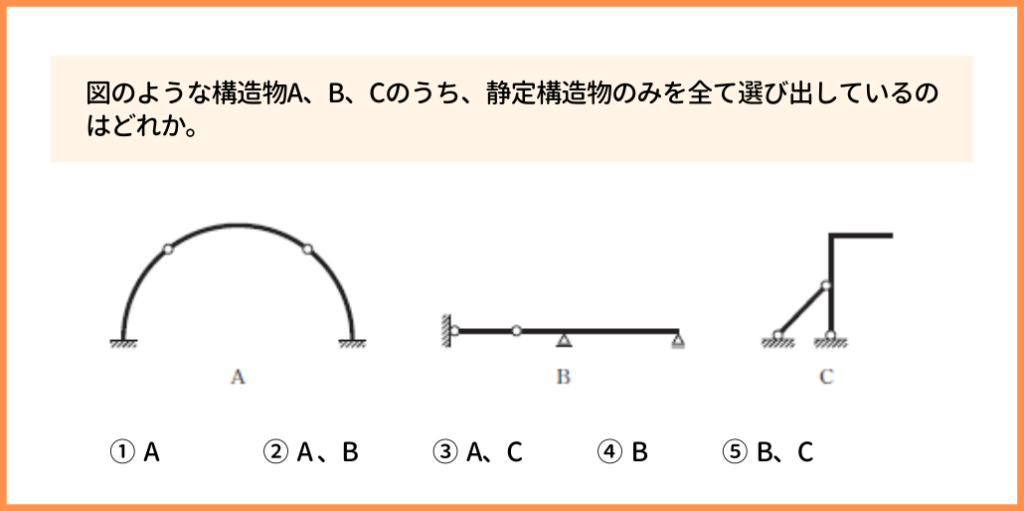
こちらも実際に国家一般職で出題されたものですが、少し難易度は高いです。
特にB、Cの考え方が難しいと思いますので、図で紹介したいと思います。
【例題③】過去問の解説
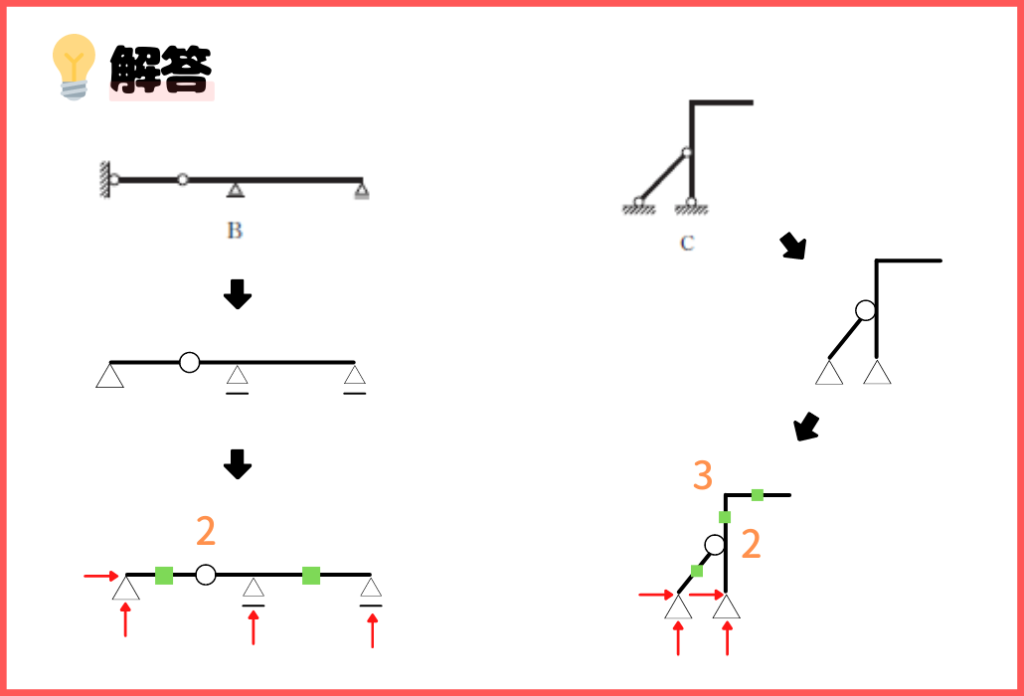
この梁の見方を変えてみると、この図のようになります!
頭の中でこのように変換できれば、後は公式に当てはめるだけですね!
不静定次数の公式は『 N=j -3m + r 』です。
- A:N=4ー3×3+6=1
- B:N=2ー3×2+4=0
- C:N=5ー3×3+4=0
N=0で静定構造物なので、答えは『 ⑤ B,C 』ですね!

考え方がわかれば超簡単なのですが、実際は解けなかった方も多いと思います。
Bは結局ただのゲルバー梁ですね!
【例題④】過去問を解いてみよう!
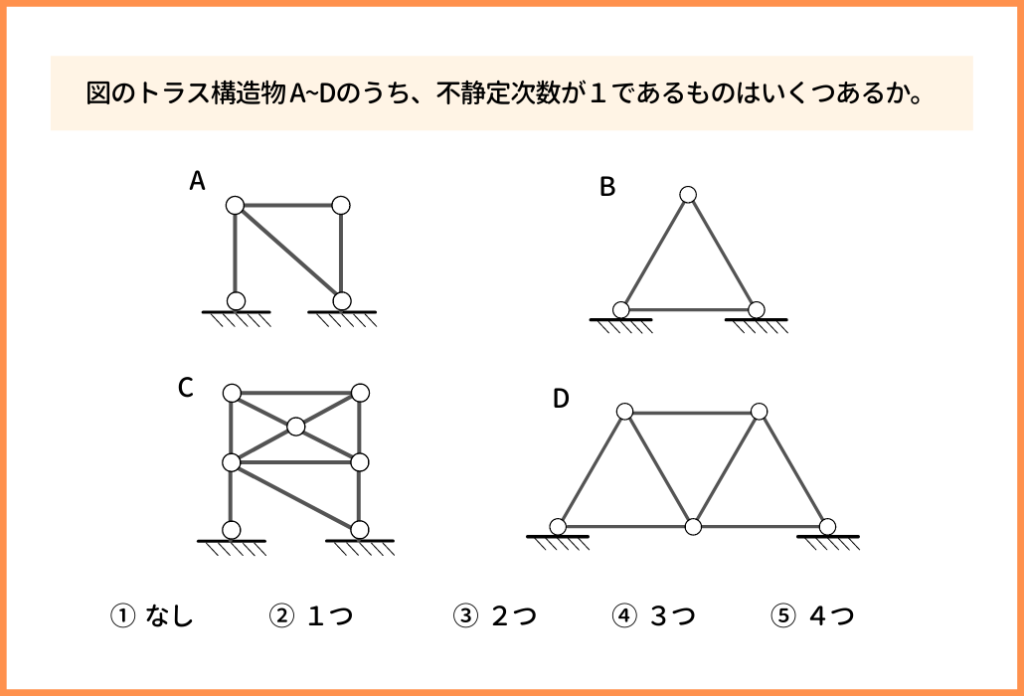
トラスの不静定次数の公式を使って解く問題です。
【例題④】過去問の解説
不静定次数の公式は『 N=m + r -2j 』です。
(mが部材数、rが反力数、jが節点数)
- A:N=4+4ー2×4=0
(部材数m=4、反力数r=4、節点数j=4)
- B:N=3+4ー2×3=1
(部材数m=3、反力数r=4、節点数j=3) - C:N=11+4ー2×7=1
(部材数m=11、反力数r=4、節点数j=7) - D:N=7+4ー2×5=1
(部材数m=7、反力数r=4、節点数j=5)
不静定次数が1であるもの(N=1)はB,C,D、答えは『 ④ 3つ 』ですね!
【例題⑤】過去問を解いてみよう!
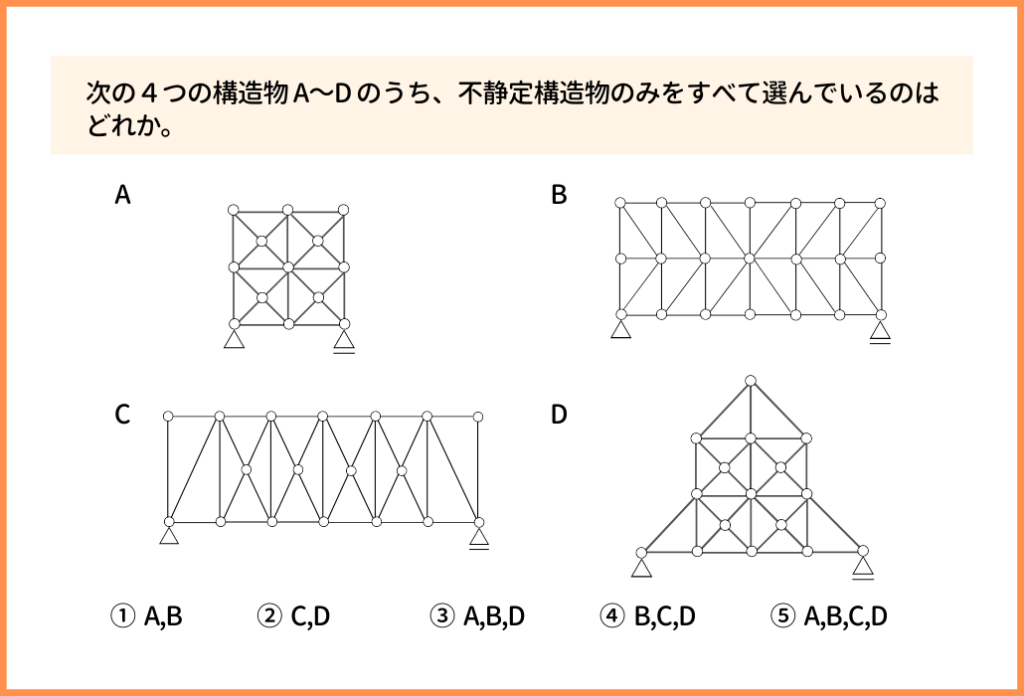
こちらもトラスの不静定次数の公式を使って解く問題です。
複雑そうに見えるかもしれませんが、公式に当てはめれば一発です!
【例題⑤】過去問の解説
不静定次数の公式は『 N=m + r -2j 』です。
(mが部材数、rが反力数、jが節点数)
- A:N=28+3ー2×13=5
(部材数m=28、反力数r=3、節点数j=13)
- B:N=44+3ー2×21=5
(部材数m=44、反力数r=3、節点数j=21) - C:N=37+3ー2×18=4
(部材数m=37、反力数r=3、節点数j=18) - D:N=35+3ー2×16=5
(部材数m=35、反力数r=3、節点数j=16)
不静定次数の値が0より大きいもの(N>0)はA,B,C,D、答えは『 ⑤ A,B,C,D 』ですね!

コメント

不静定次数の公式を使った問題を解いてみてどうだったでしょうか?
めちゃくちゃ簡単ですよね!
慣れてくるとパッと構造物を見ただけで何となく静定か不静定かわかったりするものもあります。
絶対に落としてはいけない問題なので、1問絶対に取れるように要点はおさえておきましょう!
前のテーマを勉強 | トップメニューに戻る | 次のテーマを勉強
















⇒講義資料(PDF)はこちら